1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
|
#include <iostream>
#include <fstream>
#include <eigen3/Eigen/Dense>
#include <io.h>
#include <fcntl.h>
#include <chrono>
using std::cout, std::wcout, std::endl;
using std::chrono::high_resolution_clock,
std::chrono::duration_cast, std::chrono::microseconds;
using Eigen::Matrix, Eigen::MatrixXi, Eigen::Dynamic;
using MatrixXXi = Matrix<MatrixXi, Dynamic, Dynamic>;
using MatrixXch = Matrix<wchar_t, Dynamic, Dynamic>;
const int BIT1 = 1 << 0, BIT2 = 1 << 1;
std::wostream &operator<<(std::wostream &o, const MatrixXch &m) {
for (int i = 0; i < m.rows(); ++i) {
for (int j = 0; j < m.cols(); ++j) {
o << m(i, j);
}
o << endl;
}
return o;
}
int main() {
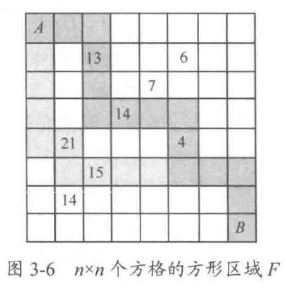
// 从文件中读取价值数据,并存入价值矩阵V中
std::ifstream in_file{"input.txt"};
int n;
in_file >> n;
const int nm = n - 1;
MatrixXi V = MatrixXi::Zero(n, n);
{
int i, j, v;
in_file >> i >> j >> v;
while (i != 0 && j != 0 && v != 0) {
V(i - 1, j - 1) = v;
in_file >> i >> j >> v;
}
}
in_file.close();
// 初始化缓存价值矩阵EV,以及方向记录矩阵D
MatrixXXi EV{n, n}, D{n, n};
for (int x1 = 0; x1 < n; ++x1) {
for (int y1 = 0; y1 < n; ++y1) {
EV(x1, y1) = MatrixXi::Zero(n, n);
D(x1, y1) = MatrixXi::Zero(n, n);
if (x1 == 0) {
D(x1, y1).setConstant(BIT1);
}
for (int y2 = 0; y2 < n; ++y2) {
D(x1, y1)(0, y2) |= BIT2;
}
}
}
// 更新函数
int mv = 0;
auto update = [&V, &EV, &D, &mv](int x1, int y1, int x2, int y2, int v, int d) {
v += V(x1, y1);
if (x1 != x2 || y1 != y2) {
v += V(x2, y2);
}
if (v > EV(x1, y1)(x2, y2)) {
EV(x1, y1)(x2, y2) = v;
D(x1, y1)(x2, y2) = d;
}
if (v > mv) {
mv = v;
}
};
// 遍历整个矩阵
auto time_start = high_resolution_clock::now();
EV(0, 0)(0, 0) = V(0, 0);
for (int s = 0; s < nm + nm; ++s) {
int op = 0, ed = s;
if (s > nm) {
op = s - nm, ed = nm;
}
for (int x1 = op; x1 <= ed; ++x1) {
for (int x2 = op; x2 <= ed; ++x2) {
int y1 = s - x1;
int y2 = s - x2;
int v = EV(x1, y1)(x2, y2);
if (x1 != nm) {
if (x2 != nm) update(x1 + 1, y1, x2 + 1, y2, v, 0);
if (y2 != nm) update(x1 + 1, y1, x2, y2 + 1, v, BIT2);
}
if (y1 != nm) {
if (x2 != nm) update(x1, y1 + 1, x2 + 1, y2, v, BIT1);
if (y2 != nm) update(x1, y1 + 1, x2, y2 + 1, v, BIT1 | BIT2);
}
}
}
}
auto time_stop = high_resolution_clock::now();
// 计算花费时间
auto duration = duration_cast<microseconds>(time_stop - time_start);
cout << "Time cost: " << duration.count() << "ms" << endl;
// 将结果写入文件中
std::ofstream out_file{"output.txt"};
out_file << EV(nm, nm)(nm, nm);
out_file.close();
// 还原路线图
wchar_t wh = L'◽', bl = L'◾';
MatrixXch M1{n, n}, M2{n, n};
M1.setConstant(wh), M2.setConstant(wh);
int x1 = nm, y1 = nm, x2 = nm, y2 = nm;
while (x1 != 0 || y1 != 0) {
M1(x1, y1) = bl, M2(x2, y2) = bl;
int d = D(x1, y1)(x2, y2);
if (d & BIT1) {
--y1;
} else {
--x1;
}
if (d & BIT2) {
--y2;
} else {
--x2;
}
}
M1(x1, y1) = bl, M2(x2, y2) = bl;
// 配置使C++可以输出Unicode
constexpr char cp_utf16le[] = ".1200"; // UTF-16 little-endian locale.
setlocale(LC_ALL, cp_utf16le);
_setmode(_fileno(stdout), _O_WTEXT);
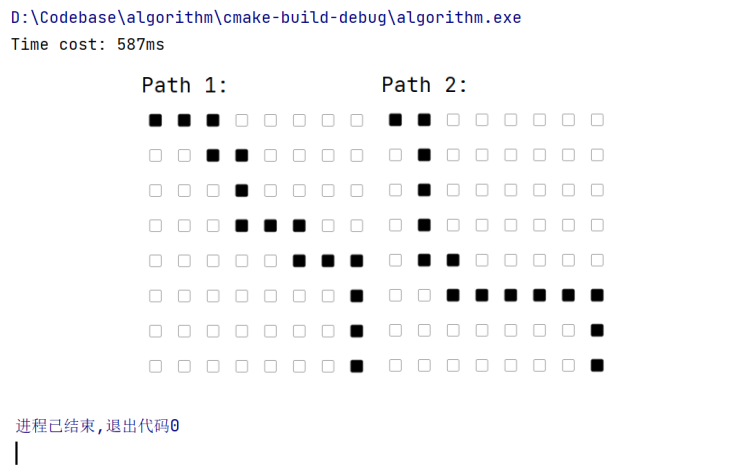
// 输出路线图
wcout << "Path 1:" << endl << M1 <<
"Path 2:" << endl << M2;
}
|